Half Adder & Full Adder Truth Table Generator
Welcome to the Half Adder & Full Adder Truth Table Generator, your go-to resource for understanding and analyzing fundamental binary addition circuits in digital electronics. You can quickly calculate Boolean outputs with this truth table tool.
Introduction to Adders
Adders are essential combinational logic circuits used in digital systems to perform arithmetic operations, particularly binary addition. They form the backbone of arithmetic logic units (ALUs), calculators, and various computing devices. The two primary types of adders are:
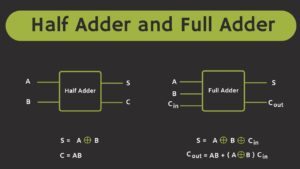
- Half Adder: Handles the addition of two single-bit binary numbers.
- Full Adder: Manages the addition of three single-bit binary numbers, including a carry-in bit from a previous addition.
How to Use the Truth Table Generator
1. Select Adder Type: Choose between Half Adder and Full Adder.
2. Input Values: Enter binary inputs (A, B, and C in for Full Adder).
3. Generate Table: Click on “Generate” to view the corresponding truth table.
4. Analyze Outputs: Study the Sum and Carry outputs for each input combination.
Truth Tables
Half Adder
| A | B | Sum (S) | Carry (C) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Logic Expressions:
- Sum (S) = A ⊕ B
- Carry (C) = A · B
Full Adder
| A | B | Cin | Sum (S) | Carry (Cout) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Logic Expressions:
- Sum (S) = A ⊕ B ⊕ Cin
- Carry (Cout) = (A · B) + (Cin · (A ⊕ B))
Applications of Adders
• Arithmetic Logic Units (ALUs): Perform arithmetic operations in processors.
• Digital Counters: Used in timekeeping and event counting.
• Binary Calculators: Facilitate binary addition in calculators.
• Data Processing Units: Handle arithmetic computations in various digital systems.
Frequently Asked Questions (FAQs)
1. What is the primary difference between a Half Adder and a Full Adder?
A Half Adder adds two single-bit binary numbers and does not account for carry-in from previous additions. In contrast, a Full Adder adds three single-bit binary numbers, including a carry-in, making it suitable for multi-bit binary addition.
2. Can a Full Adder be constructed using Half Adders?
Yes, a Full Adder can be implemented by combining two Half Adders and an OR gate. The first Half Adder adds inputs A and B, the second adds the sum from the first Half Adder with the carry-in (Cin), and the OR gate combines the carry outputs.
3. Why are adders important in digital electronics?
Adders are fundamental components in digital electronics, enabling binary addition, which is essential for arithmetic operations, data processing, and decision-making in digital systems.
4. How does the Truth Table Generator aid in learning?
The Truth Table Generator provides a visual representation of how different input combinations affect the outputs (Sum and Carry) in Half and Full Adders, enhancing understanding of binary addition logic.
Conclusion
Understanding Half and Full Adders is crucial for anyone delving into digital electronics and computer engineering. Our Truth Table Generator site offers an interactive platform to explore and comprehend the fundamental operations of these adders. Whether you’re a student, educator, or electronics enthusiast, this tool is designed to facilitate your learning and application of binary addition concepts.
